Emergent Linear Separability of Unseen Data Points in High-dimensional Last-Layer Feature Space

Abstract

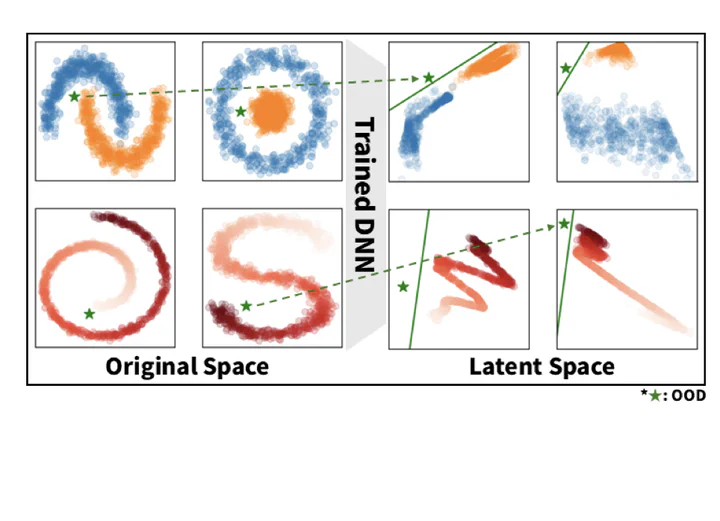
In this work, we investigate the emergence of linear separability for unseen data points in the high-dimensional last-layer feature space of deep neural networks. Through empirical analysis, we observe that, after training, in-distribution and out-of-distribution samples become linearly separable in the last-layer feature space when the hidden dimension is sufficiently high—even in regimes where the input data itself is not. We leverage these observations for the task of uncertainty quantification. By connecting our findings to classical support vector machine margin theory, we theoretically show that the separating hyperplane exhibits a higher weight norm when facing in-distribution data points. This work highlights linear separability as a fundamental and analyzable property of trained deep neural networks’ representations, offering a geometric perspective on the practical uncertainty quantification task in neural networks.

Taehun Cha

Ph.D. Candidate

There’s a cafe with my name.

Donghun Lee

Assistant Professor

Connecting artificial intelligence and mathematics, in both directions.