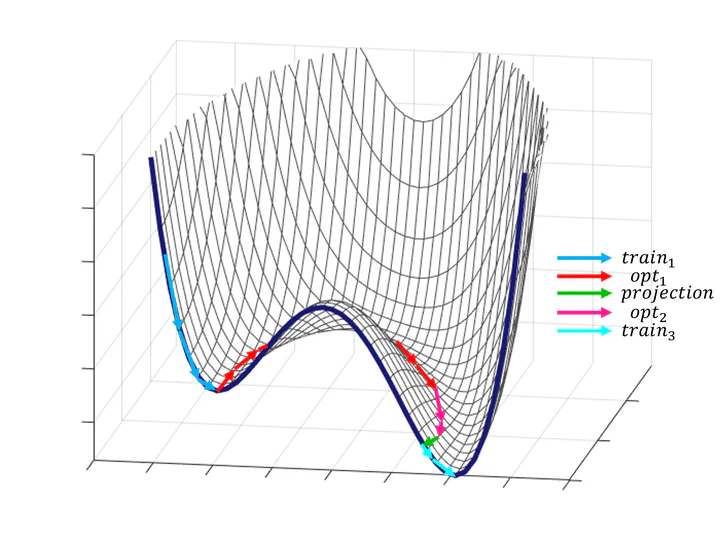
 Bypassing-in-a-nutshell diagram
Bypassing-in-a-nutshell diagramAbstract
Gradient-descent-based optimizers are prone to slowdowns in training deep learning models, as stationary points are ubiquitous in the loss landscape of most neural networks. We present an intuitive concept of bypassing the stationary points and realize the concept into a novel method designed to actively rescue optimizers from slowdowns encountered in neural network training. The method, bypass pipeline, revitalizes the optimizer by extending the model space and later contracts the model back to its original space with function-preserving algebraic constraints. We implement the method into the bypass algorithm, verify that the algorithm shows theoretically expected behaviors of bypassing, and demonstrate its empirical benefit in regression and classification benchmarks. Bypass algorithm is highly practical, as it is computationally efficient and compatible with other improvements of first-order optimizers. In addition, bypassing for neural networks leads to new theoretical research such as model-specific bypassing and neural architecture search (NAS).